How To Add Linear Expressions

Solving Linear Equations

Solving linear equations means finding the value of the variable(s) given in the linear equations. A linear equation is a combination of an algebraic expression and an equal to (=) symbol. It has a degree of 1 or information technology can be called a start-degree equation. For case, 10 + y = iv is a linear equation. Sometimes, we may have to find the values of variables involved in a linear equation. When nosotros are given two or more than such linear equations, we tin can find the values of each variable by solving linear equations. There are a few methods to solve linear equations. Let u.s. hash out each of these methods in item.

ane.	Solving Linear Equations in One Variable
2.	Solving Linear Equations by Commutation Method
three.	Solving Linear Equations by Elimination Method
4.	Graphical Method of Solving Linear Equations
5.	Cross Multiplication Method
half-dozen.	FAQs on Solving Linear Equations

Solving Linear Equations in 1 Variable

A linear equation in ane variable is an equation of caste one and has only one variable term. Information technology is of the class 'ax+b = 0', where 'a' is a non naught number and 'x' is a variable. By solving linear equations in one variable, nosotros get merely ane solution for the given variable. An example for this is 3x - 6 = 0. The variable '10' has merely 1 solution, which is calculated as
3x - 6 = 0
3x = 6
ten = 6/3
x = 2

For solving linear equations with i variable, simplify the equation such that all the variable terms are brought to one side and the abiding value is brought to the other side. If there are any partial terms and then find the LCM (Least Common Multiple) and simplify them such that the variable terms are on one side and the abiding terms are on the other side. Let us work out a minor instance to understand this.

4x + 8 = 8x - 10. To find the value of 'ten', permit us simplify and bring the 'x' terms to ane side and the constant terms to some other side.

4x - 8x = -10 - eight
-4x = -xviii
4x = 18
ten = 18/four
On simplifying, we get x = 9/two.

Solving Linear Equations by Substitution Method

The substitution method is one of the methods of solving linear equations. In the substitution method, nosotros rearrange the equation such that one of the values is substituted in the second equation. Now that we are left with an equation that has just 1 variable, we tin can solve information technology and discover the value of that variable. In the 2 given equations, any equation tin can be taken and the value of a variable can exist found and substituted in some other equation. For solving linear equations using the substitution method, follow the steps mentioned below. Let united states understand this with an example of solving the following system of linear equations.

x + y = six --------------(i)
2x + 4y = 20 -----------(2)

Step 1: Notice the value of i of the variables using any i of the equations. In this example, allow the states find the value of 'x' from equation (1).
x + y = vi ---------(1)
x = 6 - y

Pace 2: Substitute the value of the variable found in step 1 in the second linear equation. Now, permit us substitute the value of 'x' in the second equation 2x + 4y = 20.

x = 6 - y
Substituting the value of '10' in 2x + 4y = 20, nosotros get,

two(vi - y) + 4y = 20
12 - 2y + 4y = 20
12 + 2y = 20
2y = 20 - 12
2y = 8
y = 8/two
y = 4

Stride 3: Now substitute the value of 'y' in either equation (1) or (2). Let united states substitute the value of 'y' in equation (ane).

x + y = six
x + 4 = half dozen
10 = 6 - iv
ten = two

Therefore, by commutation method, the linear equations are solved, and the value of x is 2 and y is 4.

Solving Linear Equations by Elimination Method

The elimination method is another fashion to solve a organisation of linear equations. Hither we brand an attempt to multiply either the 'ten' variable term or the 'y' variable term with a constant value such that either the 'x' variable terms or the 'y' variable terms cancel out and gives us the value of the other variable. Let u.s. understand the steps of solving linear equations past elimination method. Consider the given linear equations:

2x + y = xi ----------- (i)
ten + 3y = eighteen ---------- (2)

Step 1: Check whether the terms are arranged in a fashion such that the 'x' term is followed by a 'y' term and an equal to sign and after the equal to sign the abiding term should be present. The given set of linear equations are already arranged in the right way which is ax+by=c or ax+by-c=0.

Step 2: The next stride is to multiply either one or both the equations by a constant value such that it will brand either the 'x' terms or the 'y' terms cancel out which would assist the states find the value of the other variable. Now in equation (two), let u.s. multiply every term by the number ii to brand the coefficients of ten the same in both the equations.

x + 3y = 18 ---------- (2)

Multiplying all the terms in equation (2) by 2, we get,

ii(x) + 2(3y) = 2(18). At present equation (two) becomes,

2x + 6y = 36 -----------(2)

Step 3: The next step is to simplify these two equations by adding or subtracting them (whichever operation is required to cancel the x terms). Now, by subtracting the two equations, nosotros can cancel out the 'x' terms in both equations.

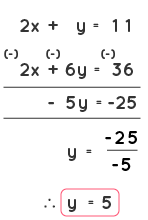
Elimination Method of solving linear equations

Therefore, y = 5.

Step four: Using the value obtained in pace iii, find out the value of another variable by substituting the value in any of the equations. Let us substitute the value of 'y' in equation (one). We get,

2x + y = xi
2x + 5 = 11
2x = 11 - five
2x = half-dozen
x = 6/2
10 = 3

Therefore, by solving linear equations, we get the value of x = 3 and y = v.

Graphical Method of Solving Linear Equations

Some other method for solving linear equations is by using the graph. When we are given a organisation of linear equations, nosotros graph both the equations by finding values for 'y' for unlike values of 'x' in the coordinate organization. Once it is done, we find the point of intersection of these two lines. The (10,y) values at the betoken of intersection give the solution for these linear equations. Let us accept two linear equations and solve them using the graphical method.

ten + y = 8 -------(one)

y = x + 2 --------(2)

Let us take some values for 'x' and find the values for 'y' for the equation ten + y = 8. This can besides be rewritten equally y = eight - x.

ten	0	1	2	3	4
y	eight	7	half-dozen	5	iv

Let us take some values for 'x' and find the values for 'y' in the equation y = x + two.

ten	0	1	2	three	iv
y	2	3	4	5	6

Plotting these points on the coordinate plane, we get a graph similar this.

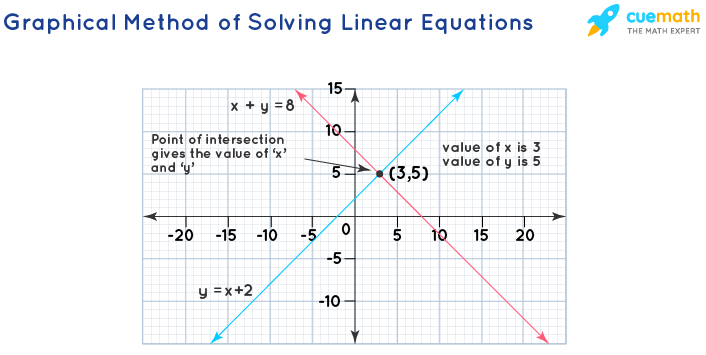
Graphical Method of Solving Linear Equations

Now, nosotros find the point of intersection of these lines to detect the values of 'x' and 'y'. The 2 lines intersect at the point (3,5). Therefore, ten = 3 and y = 5 past using the graphical method of solving linear equations.

This method is also used to find the optimal solution of linear programming problems. Let us look at one more method of solving linear equations, which is the cross multiplication method.

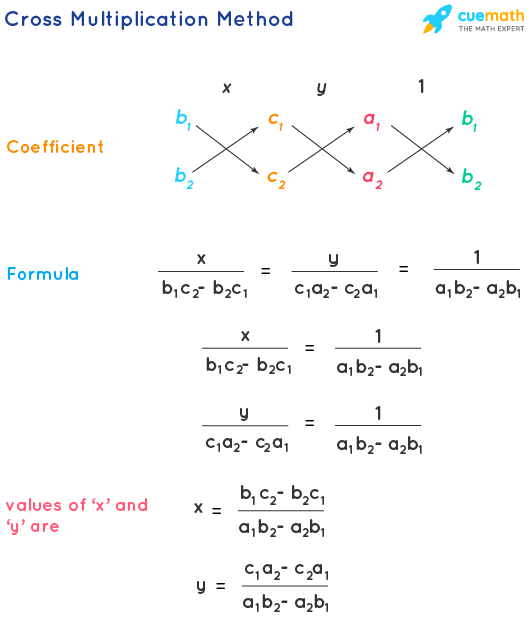
Cantankerous Multiplication Method of Solving Linear Equations

The cross multiplication method enables us to solve linear equations past picking the coefficients of all the terms ('x' , 'y' and the constant terms) in the format shown below and apply the formula for finding the values of 'x' and 'y'.

Cross Multiplication Method of solving linear equations

Topics Related to Solving Linear Equations

Bank check the given articles related to solving linear equations.

Linear Equations
Application of Linear Equations
Two-Variable Linear Equations
Linear Equations and Half Planes
One Variable Linear Equations and Inequations

Solving Linear Equations Examples

Example one: Solve the following linear equations by the substitution method.

3x + y = 13 --------- (one)
2x + 3y = 18 -------- (2)

Solution:

By using the substitution method of solving linear equations, let us accept the showtime equation and observe the value of 'y' and substitute it in the second equation.

From equation (one), y = 13-3x.
Now, substituting the value of 'y' in equation (2), we get,
2x + iii (13 - 3x) = xviii
2x + 39 - 9x = xviii
-7x + 39 = 18
-7x = 18 - 39
-7x = -21
x = -21/-7
x = 3
Now, allow us substitute the value of 'x = 3' in equation (one) and notice the value of 'y'.
3x + y = 13 ------- (1)
3(3) + y = 13
9 + y = 13
y = xiii - 9
y = 4

Therefore, by the commutation method, the value of x is 3 and y is 4.
Instance 2: Using the elimination method of solving linear equations find the values of 'ten' and 'y'.

3x + y = 21 ------ (one)
2x + 3y = 28 -------- (2)

Solution:

By using the elimination method, allow united states brand the 'y' variable to be the same in both the equations (1) and (2). To exercise this permit the states multiply all the terms of the first equation by 3. Therefore equation (1) becomes,

three(3x) + three(y) = 63
9x + 3y = 63 ---------- (iii)
The 2d equation is,
2x + 3y = 28
Now permit us cancel the 'y' terms and detect the value of 'x' past subtracting equation (2) from equation (3). This is done by changing the signs of all the terms in equation (two).

Substituting the value of x = 5 in equation (one) we become,
3x + y = 21 --------(one)
three(5) + y = 21
15 + y = 21
y = 21 - 15
y = 6

Therefore, by the elimination method, the value of ten is 5 and y is half dozen.
Example 3: Using the cross multiplication method of solving linear equations, solve the post-obit equations.

x + 2y - xvi = 0 --------- (1)
4x - y - 10 = 0 ---------- (2)

Solution:

Compare the given equation with \(a_{one}\)10 + \(b_{1}\)y + \(c_{1}\) = 0, and \(a_{2}\)10+\(b_{2}\)y+\(c_{2}\) = 0. From the given equations,

\(a_{1}\) = 1, \(a_{ii}\) = 4, \(b_{one}\) = 2, \(b_{ii}\) = -1, \(c_{one}\) = -xvi, and \(c_{2}\) = -10.

By cross multiplication method,

ten = \(b_{one}\)\(c_{two}\) - \(b_{2}\)\(c_{1}\)/\(a_{ane}\)\(b_{2}\) - \(a_{2}\)\(b_{1}\)
y = \(c_{1}\)\(a_{2}\) - \(c_{2}\)\(a_{1}\) / \(a_{1}\)\(b_{2}\) - \(a_{two}\)\(b_{ane}\)

Substituting the values in the formula we become,

x = ((2)(-10)) - ((-one)(-16)) / ((ane)(-one)) - ((iv)(two))
x = (-20-16)/(-1-8)
x = -36/-9
x = 36/9
x = 4
y = ((-xvi)(iv)) - ((-10)(1)) / ((ane)(-1)) - ((4)(2))
y = (-64 + x) / (-i - 8)
y = -54 / -9
y = 54/9
y = half-dozen

Therefore, by the cantankerous multiplication method, the value of x is 4 and y is 6.

become to slidego to slidego to slide

Breakdown tough concepts through elementary visuals.

Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

Exercise Questions on Solving Linear Equations

go to slidego to slidego to slide

FAQs on Solving Linear Equations

What does it Mean by Solving Linear Equations?

An equation that has a degree of one is called a linear equation. We can have one variable linear equations, two-variable linear equations, linear equations with three variables, and more depending on the number of variables in it. Solving linear equations ways finding the values of all the variables present in the equation. This can be washed past exchange method, elimination method, graphical method, and the cross multiplication method. All these methods are different means of finding the values of the variables.

How to Utilize the Exchange Method for Solving Linear Equations?

The substitution method of solving equations states that for a given organization of linear equations, find the value of either '10' or 'y' from whatsoever of the given equations so substitute the value constitute of 'x' or 'y' in another equation and so that the other unknown value can be institute.

How to Use the Elimination Method for Solving Linear Equations?

In the elimination method of solving linear equations, nosotros multiply a constant or a number with one equation or both the equations such that either the 'x' terms or the 'y' terms are the aforementioned. And then we cancel out the same term in both the equations by either adding or subtracting them and find the value of one variable (either 'ten' or 'y'). After finding one of the values, we substitute the value in 1 of the equations and observe the other unknown value.

What is the Graphical Method of Solving Linear Equations?

In the graphical method of solving linear equations, we find the value of 'y' from the given equations by putting the values of 10 equally 0, one, two, iii, and so on, and plot a graph in the coordinate system for the line for diverse values of 'x' for both the arrangement of linear equations. We will come across that these two lines intersect at a point. This point is the solution for the given system of linear equations. If in that location is no intersection point between 2 lines, so nosotros consider them equally parallel lines, and if we found that both the lines lie on each other, those are known as coincident lines and accept infinitely many solutions.

What are the Steps of Solving Linear Equations that has I Variable?

A linear equation is an equation with degree 1. To solve a linear equation that has ane variable nosotros bring the variable to 1 side and the constant value to the other side. Then, a non-zero number may be added, subtracted, multiplied, or divided on both sides of the equation. For example, a linear equation with ane variable will exist of the grade 'x - 4 = two'. To find the value of 'x', we add the constant value '4' to both sides of the equation. Therefore, the value of 'x = 6'.

What are the Steps of Solving Linear Equations having Three Variables?

To solve a system of linear equations that has three variables, we take any two equations and variables. We then take another pair of linear equations and also solve for the same variable. Now that, we accept two linear equations with two variables, we tin can employ the substitution method or emptying method, or any other method to solve the values of two unknown variables. Later finding these two variables, we substitute them in any of the three equations to find the 3rd unknown variable.

What are the 4 Methods of Solving Linear Equations?

The methods for solving linear equations are given below:

Exchange method
Elimination method
Cross multiplication method
Graphical method